Формулата што секое дете ја учи е: a² + b² = c². Вавилонците користеле тригонометрија за мерење на земјиштето пред 3.700 години, што значи илјада години пред Питагора.
Мистериозна глинена плоча може да направи револуција во историјата на математиката.
Ископана е во 1984 година во близина на денешен Багдад, но потоа е заборавена во аголот на Археолошкиот музеј во Истанбул.
Во 2018 година, австралискиот математичар Даниел Менсфилд од Универзитетот во Нов Јужен Велс наишол на фотографија од објектот и веднаш бил изненаден од неговите совршени прави агли. Тој отпатувал во Турција и ја анализираше мистериозната табла.
Сега ја реши загатката.
Таблетата стара 3.700 години од древната вавилонска ера не е само најстариот познат доказ за применета геометрија, туку ја содржи и доктрината за триаголници што му ја припишуваме на Питагора.

Дали Питагора го препишал своето учење?
Според студијата „Plimpton 322: A Study of Rectangles“ објавена во списанието „Foundations of Science“, историјата на математиката можеби ќе треба да се препише.
„Откривањето и анализата на оваа табла имаше важни последици за историјата на математиката“, рече Даниел Менсфилд за Сиднеј Морнинг Хералд.
Бидејќи, до сега, се сметаше дека тригонометријата ја развиле старите Грци, поточно – Питагора. Но, новата анализа покажа дека тригонометријата била позната илјада години пред Питагора.
Дропки наместо агли
Уште во 2017 година, Менсфилд објави многу интересна студија за друго парче глина. Тоа беше најстарата позната тригонометриска табела напишана со клинесто писмо.
Според Менсфилд, пресметките на Вавилонците биле многу попрецизни од грчките, бидејќи тие не се базирале на аглите или функциите на кругот, туку на односите меѓу броевите.
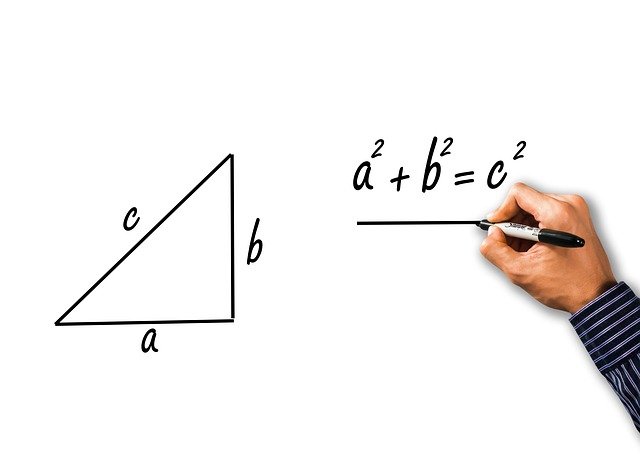
Слично на нашата пресметка на времето, Вавилонците користеле броење врз основа на бројот 60, што резултираше со тоа што нивните дропки даваат цели броеви многу почесто и има помалку грешки при заокружување.
Таа табла со големина на разгледница, наречена Plimpton 322, потекнува од истото вавилонско време, но досега не е откриено за што служела оваа серија броеви. Се претпоставуваше дека може да се користела за изградба на куќи или мерни полиња.
Оваа претпоставка сега е потврдена со мала скршена плоча од древното вавилонско време: тркалезна плоча со ознака Si.427 содржи правни и геометриски детали за парче земја што било поделено откако бил продаден еден дел. Тоа е, така да се каже, катастарски документ во кој се утврдени точните граници на имотот.
Практична корист
„Овој нов одбор ни покажа зошто биле заинтересирани за геометрија: за да можат точно да ги одредат границите на поседите на земјиштето“, вели д -р Менсфилд.
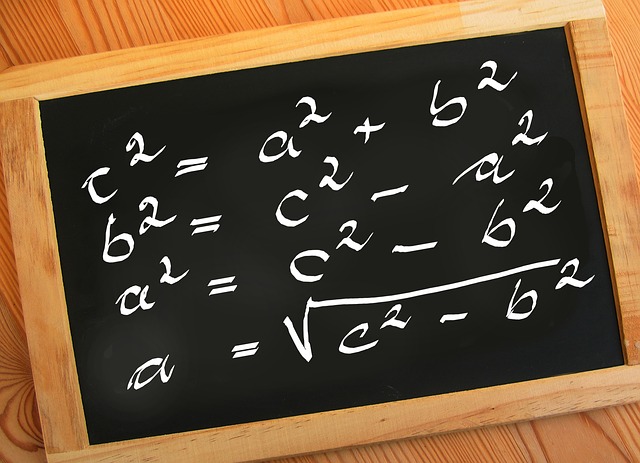
За да се одреди површината на земјиштето, геодет требало да дојде на прво место, да го измери имотот и да ги утврди неговите граници “.
Истражувачите користеле „Питагорски тројки“ за точно да го пресметаат вистинскиот агол, и овие тројки се состојат од по три природни броеви, кои можат да послужат како должини на страните на правоаголниот триаголник (пр. Тројки 5,6,7). Одредуваат и прави агли.
Решен соседски спор
„Таблата датира од времето кога земјата постепено се префрлала во приватна сопственост – луѓето почнале да размислуваат за сопственоста на земјиштето„ на своја или „туѓа“и сакале да се оцртаат токму за да бидат во добрососедски услови“, вели Менсфилд. И оваа табла веднаш го покажува тоа: поле што е поделено и на кое се исцртани нови граници “.
Менсфилд известува дека има повеќе древни вавилонски плочи на кои може да се види слична постапка. Еден од нив, на пример, е напишан по повод спор за скапоцени палми со урми што се наоѓале помеѓу две земјишни стопанства.
Локалниот управител ги повикувал геодетите да ги решат споровите.
„Ова јасно покажува колку точноста на мерењата била важна во решавањето на споровите меѓу моќните луѓе во тоа време“, вели Менсфилд.
Комплексна геометрија со практична употреба – илјада години пред раѓањето на Питагора.

